Функциональный элемент с n упорядоченными входами и одним выходом.
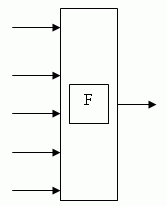
При подаче на выходы любой комбинации двоичных сигналов, на выходе также возникает сигнал.
Каждый вход – аргумент функции.
Выход – булева функция от аргументов.
Из функциональных элементов можно строить по правилам их соединения схемы (логические сети).
Два и более входов можно отождествлять.
Возможные соединения функциональных элементов соответствуют булевым функциям и их суперпозициям.
Полный набор булевых функций, который мы будем использовать для построения логических сетей (схем) в какой-нибудь задаче, мы назовем базисом из функциональных элементов.
Число функциональных переменных считаем сколь угодно большим.
Базис называется полным, если с его помощью можно реализовать любую булеву функцию в виде схемы.
Очевидно, чтобы базис был полным, необходимо и достаточно, чтобы система функций, реализуемых элементами базиса, была полной.
Пример полного базиса.
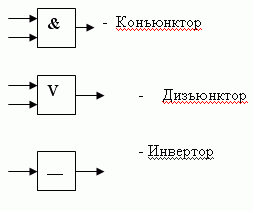
Чтобы построить минимальную функциональную схему для функции на конъюнкторах, дизъюнкторах и инверторах, которая реализует эту функцию, нужно
1. Найти минимальную ДНФ.
2. Для любой из минимальных ДНФ (их может быть много) попробовать упростить формула с помощью вынесения за скобки общего множителя.
Сумматор n-разрядных двоичных чисел
Составить элементы с 2n входами и n+1 выходом, реализующих сложение n-разрядных двоичных чисел вида
X = XnXn-1…X1
Y = YnYn-1…Y1
Z = x+y = Zn+1Zn…Z1
X+Y – сумма чисел.
Для решения такой задачи вводим qi – единица переноса из одного разряда в другой.
Формулы сумматора
Zi = Xi + Yi + Qi – сумма по модулю 2
Qi+1 = XiYi V XiQi V QiYi