R - множество действительных чисел.
X e R - элемент X принадлежит множеству R.
Равные множества - множества, состоящие из одинаковых элементов.
A = B - множество А равно множеству B.
0 - пустое множество.
A<= C - Множество А является подмножеством множества С.
Если А не равно С и А <= C, то А < С. (строго).
Если A <= C и C <= А, то А = С.
Пустое множество 0 является подмножеством любого множества.
Существуют конечные и бесконечные множества. Пусть n - число элементов данного множества А. Это число называется мощностью данного множества.
У множества рациональных чисел мощность является счетной (т.е. все элементы можно пронумеровать).
У множества иррациональных чисел мощность - континиум. Обозначается (С).
Основное правило комбинаторики (показано на примере)
Пусть имеется палочка, разделенная на 3 части. Первую ее часть можно раскрасить n способами, вторую - m, третью - k. Всего способов раскраски палочки - n*m*k. Аналогично с множествами
U = {a1,a2… an-1, an}
Пусть U = {a1, a2, a3}
Выпишем множество всех подмножеств множества U.
P(U) = {0, a1, a2, a3, a1a2, a1a3, a2a3, a1a2a3}.
Мощность множества U равна 3, а мощность P(U) равна 8.
Методом математической индукции доказывается, что при произвольной мощности n множества U, мощность множества P(U) равна 2n.
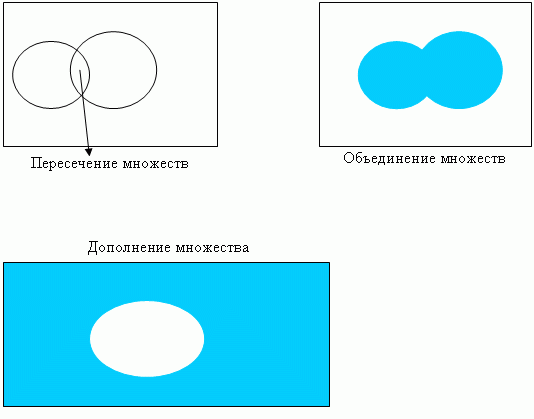
Операции над множествами
1. Объединение множеств (A U B). Элемент, принадлежащий полученному множеству, принадлежит множеству А ИЛИ множеству В.
2. Пересечение множеств (A n B). Элемент, принадлежащий полученному множеству, принадлежит множеству А И множеству В.
3. Дополнение множества А. (С = А ) - не А. Все элементы, принадлежащие универсальному множеству, не принадлежат множеству А.
Свойства операций над множествами.
1. A U B = B U A - коммутативность . A n B = B n A
2. (A U B) U C = A U (B U C), A n (B n C) = (A n B) n C - ассоциативность.
3. (A U B) n C = (A n C) u (B n C), (AnB) U C = (A U C) n (B U C) - дистрибутивность.
4. Поглощение A U A = A, A n A = A.
5. Существование универсальных границ. А U 0 = A A n 0 = 0 A u U = U A n U = A
6. Двойное дополнение
7. A U
8. Законы двойственности или закон Де - Моргана