Носитель элементарной конъюнкции ранга R будем называть интервалом ранга R.
Интервал ранга R содержит 2N-R векторов.
N – количество рассматриваемых векторов.
Интервал – носитель элементарной конъюнкции.
Теорема
Носитель дизъюнкции двух функций равен объединению носителей этих функций.
Доказательство.
Носитель ДНФ является объединением интервалов.
Допустимым интервалом для данной функции называется интервал, который целиком содержится в носителе этой функции.
Nf = I1 V I2 V … V Ik
Интервал для данной функции является максимальным, если он не содержится целиком ни в каком другом допустимом интервале.
Элементарная конъюнкция, носителем которой является допустимый интервал, называется импликантой.
ЭК, N – максимальный интервал – простая импликанта.
Представление носителя в виде объединения максимальных интервалов будем называть покрытием носителя максимальными интервалами.
Дизъюнкция всех возможных простых импликант называется сокращенной ДНФ функции.
Покрытие носителя интервалами будем называть неприводимым, если ни один нельзя отбросить из правой части равенства, не нарушив это равенство.
ДНФ, которая соответствует неприводимому покрытию, называется тупиковой ДНФ.
Утверждение.
Минимальная ДНФ содержится среди тупиковых ДНФ.
Определение
Максимальный интервал называется ядровым, если он содержит хотя бы одну вершину из носителя функции, которая не принадлежит больше никакому другому максимальному интервалу.
Элементарная конъюнкция, соответствующая ядровому интервалу – ядровая импликанта.
Объединение всех ядровых интервалов – ядро функции.
Дизъюнкция всех ядровых импликант - ядровая ДНФ.
Ядро функции обязательно входит в любое неприводимое покрытие.
Алгоритм получения минимальной ДНФ.
1. Выделяем носитель функции.
2. Выделяем все возможные интервалы.
3. Выписываем все простые импликанты.
4. Выделяем ядровый интервал.
5. Используя ядро функции и комбинацию неядровых интервалов, получаем все неприводимые покрытия, для каждого из которых выписываем тупиковую ДНФ.
6. Среди тупиковых ДНФ выбираем минимальную.
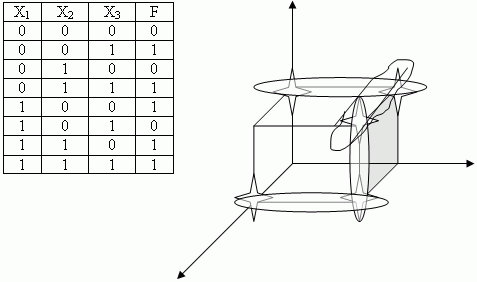
Выделение всех возможных интервалов.
1. Для булева куба размерности 3 интервалом ранга 1 могут быть 4 вершины, лежащие в одной грани.
2. Ранга 2 – любые 2 вершины, соединенные ребром.
3. Ранга 3 – любая отдельная вершина.
1. Нет _
2. I1 = { 001 011} <-> П1 = x1x3 - ядровый
I2 = { 011 111} <-> П2 = x2x3
Если координата вектора меняет значения, то переменная не входит
I3 = { 111 110} <-> П3 = x1x2
_
I4 = { 110 100} <-> П4 = x1x3
Dсокр. = П1 V П2 V П3 V П4
Nf = I1 U I4 U I2 (U – объединение)
Получили неприводимое покрытие, добавив к ядру недостающие интервалы так, чтобы все единичные вершины были задействованы.
D1= П1 V П4 V П2
Nf = I1 U I4 U I3
D2= П1 V П4 V П3
Сосчитаем ранги тупиковых ДНФ
R1 = 6
R2 = 6
Dmin = D1 = D2
Метод карт Карно для нахождения минимальной ДНФ
n = 4
Карта Карно – плоскостная интерпретация 4-мерного булева куба.
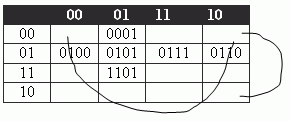
Считаем, что левый край склеен с правым, а верхний – с нижним.
Если таблицу Карно свернуть таким образом, то получится тор (torus - геометрическая фигура, напоминающая бублик).
Правила поиска интервалов.
1. Интервалом ранга 1 могут быть 2 соседних строки (2 соседних столбца)
2. Интервалом ранга 2 может быть вся строка, весь столбец или квадрат 2х2.
3. Интервалом ранга 3 – любые 2 соседние по горизонтали и вертикали клетки.
4. Одна отдельно взятая вершина будет интервалом ранга 4.
Алгоритм – тот же самый.