V – вершина орграфа
M-(V) – множество ребер, для которых вершина V является концом.
M+(V) – множество ребер, для которых вершина V является началом.
Транспортной сетью называется связный орграф без петель, для которого выполнены следующие условия
1. Существует только одна вершина A, для которой M-(А) – пустое множество. А – исток.
2. Имеется только одна вершина B, для которой M+(B) – пустое множество. В – сток.
3. Каждому ребру графа поставлено в соответствие целое неотрицательное число, называемое пропускной способностью данного ребра.
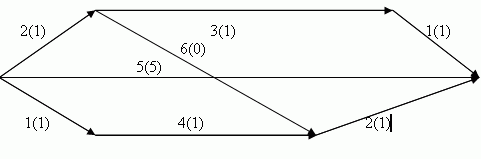
Потоком в транспортной сети (ТС) называется целочисленная функция, определенная на любых ребрах ТС и удовлетворяющая следующим свойствам
1. ф(X) <= C(X), где С(X) – пропускная способность ребра.
На всех ребрах значение функции потока не превосходит значения пропускной способности ребра. Значение функции потока ставим рядом со значением пропускной способности ребра в скобках.
2. Для каждой внутренней вершины V транспортной сети, не равной A или B выполняется следующее условие: суммарная функция потока по ребрам, входящим в вершину, равна суммарной функции потока по ребрам, исходящим из вершины (сколько втекает, столько и вытекает).
Величиной потока [ф] = val(ф) называется число, равное сумме функций потока по всем ребрам, выходящим из вершины А или сумма всех функций потока по всем ребрам, входящим в вершину В.
Выбор потока.
1. Берем путь из А в В.
2. Выбираем минимальную пропускную способность и ставим ее в соответствие каждому ребру из пути.
3. Просматриваем все остальные ребра. Если они не пересекаются, то проделываем для них то же самое, начиная с п1. Всем остальным ребрам ставим в соответствие значение функции потока, равное 0.
Поток в транспортной сети называется максимальным, если выполнено условие
Val(ф) больше Val(Ф*)
Ф* = maximum
Любое подмножество S транспортных вершин, содержащих исток и не содержащих сток, определяет разрез, отделяющий исток от стока (разрез).
Разрез состоит из всех вершит тех ребер, которые имеют свои начала в вершинах множества S, а концы – из дополнения к множеству S.
Пропускной способностью разреза K называется сумма значений пропускных способностей всех ребер этого разреза.
Разрез K** называется минимальным, если для любого другого разреза выполнено условие C(K**) C(K).
Теорема Форда – Фалькерсона (без доказательства).
В транспортной сети величина максимального потока равна пропускной способности минимального разреза.
Алгоритм нахождения максимального потока (Алгоритм Форда – Фалькерсона).
1. Берем любой поток в транспортной сети.
2. Строим граф перестроек g* по следующему правилу:
В него входят все вершины исходного графа g.
Те ребра, на которых значение функции потока в исходном графе g были равны 0, входят в новый граф без изменений со своими пропускными способностями.
Все ребра, на которых ф(x) > 0 в новом графе g* заменяются двумя ребрами x* и x**. Ребро x* направлено в ту же сторону, что и x, и пропускная способность c(x*) = c(x) – ф(x).
Ребро x** направлено в противоположную сторону ребру x, и пропускная способность c(x**) = ф(x).
Ребра с нулевой пропускной способностью можно не рисовать.
3. В графе g* ищем путь из А в В по ребрам с ненулевой пропускной способностью. Если его нет, то имеющийся поток является максимальным и алгоритм закончен. Иначе переходим к пункту 4.
4. Меняем значение функции потока в графе g для тех ребер, которые соответствуют найденному пути в графе перестроек по следующему правилу:
Если направление ребра x в графе g совпадает с направлением пути, то новое ф(x) = ф(x) + z
Если же направление противоположно направлению пути, то ф(x) = ф(x) - z
5. Переходим на шаг 2 с новым потоком.